A Turing machine is an FSM that controls one or more tapes, where at least one tape is of unbounded length (i.e. infinitely long)
Background
- In the early twentieth century, mathematicians were trying to find a universal machine – a mathematical model that consisted of a small number of basic operations and a machine that could perform all these operations.
- The machine would then be able to run any algorithm.
- This model would be a precise definition of the term algorithm. The hope was to find algorithms that would be able to solve all mathematical problems.
Solvable and unsolvable problems
- Alan Turing was a British Mathematician who, in 1936, wrote a paper called ‘On Computable Numbers’.
- This paper introduced the concept of the Turing machine – a universal machine capable of solving any problem that can be represented algorithmically.
- He used his machine to show that it is not possible to determine if any given problem has a solution, or not. This has serious implications in computing. It means that it may not always be possible to determine if a particular problem is unsolvable, or if it has just not been solved yet.
Turing Machine
- An input alphabet.
- A tape that is infinitely long.
- An output alphabet that can be printed on the tape.
- A tape head that is used to read/write to the cells.
- A finite set of states, including a start state.
- A program (set of instructions)
- A Turing machine describes an algorithm.
- A computer uses a computer program that is basically an algorithm.
- Turing machines therefore can be used to run and look at algorithms independent of the architecture of a particular machine.
- An algorithm running on a particular machine will have had to make decisions about how to store values (e.g. the precision of how to store a real number).
- This does not happen on a Turing machine, meaning a Turing machine is a more general representation of the algorithm.
 |
| Transition Rules for a Turing Machine |
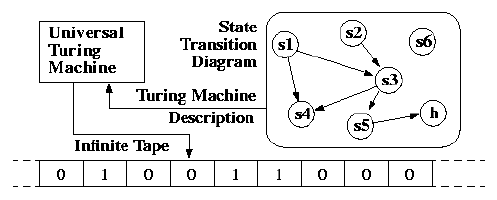 |
| Overview of a Turing Machine |


No comments:
Post a Comment